1. INTRODUCTION
Given the huge size of the Web graph, computing rankings of Web pages requires awesome resources—computations on matrices whose size is of the order of the size of the Web (109 nodes). Moreover, the ranking algorithm should be applied on recent Web graph snapshots to guarantee fresh and accurate results, which implies continuous crawling. This requirement poses a tough problem as it is practically impossible to crawl the whole Web graph in reasonable time intervals due to its huge size and dynamic nature.
Thus, given a high quality page ranking prediction mechanism, with known temporal robustness (i.e., prediction accuracy deterioration with time), a search engine can optimize its resources and schedule crawling efforts at times when the prediction accuracy falls under a threshold. Another important industry motivating rank predictions is advertising: pages with future high rank are attractive for placing advertisements.
In this paper we propose a framework that enables prediction of the ranking of Web pages, based on previous rank positions. We capitalize on trends of the Web pages through the rank change rate (racer) among different snapshots of the Web graph. We evaluate the prediction quality based on the similarity of the predicted ranked lists to the actual ones. We focus on the top-k elements of ranked list of Web pages, since these pages are more important for Web search.
The problem of predicting PageRank is partly addressed in [4], which focuses on Web page classification based on URL features. The authors report experiments for PageRank predictions using the extracted features using linear regression; however, the complexity of this approach grows linearly in proportion to the number of features used. An approach that aims at approximating PageRank values without the need of performing the computations over the entire graph is that of Chien et al. [1]. The authors propose an efficient algorithm to incrementally compute approximations to PageRank, based on the evolution of the link structure of the Web graph. In [2] there is an algorithm that offers estimates of cumulative PageRank scores.
2. THE PREDICTIONS FRAMEWORK
Rank Change Rate
In order to predict future rankings of Web pages, we have adopted a measure (racer) we introduced in [5] for measuring page rank dynamics. It is defined as racer(p,ti) = 1 − nrank(p,ti+1) ⁄ nrank(p,ti) where nrank(p,ti) is the normalized rank of page p at time ti.
Given a set of successive Web graph snapshots, for each page we generate a sequence of rank change rates that indicates the trends of this page among the previous snapshots. We use these sequences of previous snapshots of the Web graph as a training set for learning predictors to forecast the trends of a Web pages, with the following phases:
a. Computing rank trends
We assume a set of successive Web graph snapshots crawled at different timestamps. Each Web page is associated with a rank position, indicating its importance in the particular snapshot. Thereafter, we compute racer as a measure of the page's rank trends.
 |
 |
 |
 |
| (a) OSim for DBLP | (b) KSim for DBLP | (c) OSim for Internet Archive | (d) KSim for Internet Archive |
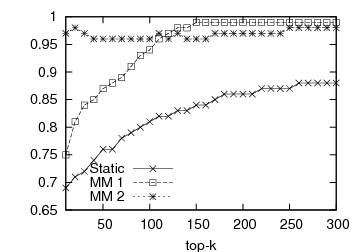
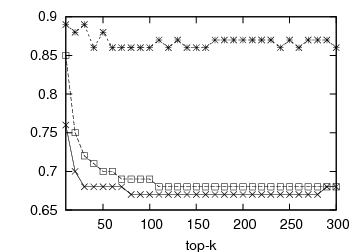
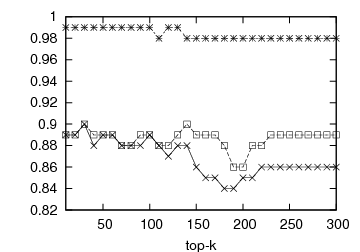
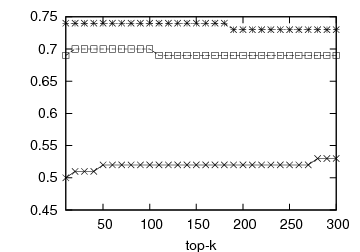
Figure 1: Prediction accuracy vs top-k list length: DBLP and Internet Archive datasets
b. Markov Model (MM) states learning
To ensure that the accuracy and the coverage of the MM is high, distinct values appearing in rank change sequences are reduced to a manageable size by mapping each value to a representative equi-probable value. These are used as states of the MM.
Assuming d distinct racer values R = {r1, … , rd} and the corresponding frequencies of each data value F = {f1, … , fd} the objective is to partition the data range [r1, rd] of R into n non-overlapping adjacent partitions Ri each corresponding to a data range [rli, rui], with rli, rui the lower and the upper value of the Ri data range. Our algorithm takes as an input the set of the distinct racer values R and their frequencies F and returns the set S of the states of the Markov Model.
After conducting enough experiments, we chose to fix the cardinality of the MM set of states to n=50, which led to a reasonable prediction accuracy. The MM is trained based on previous snapshots of the Web graph and is used to predict the future rank of a Web page, by matching its current ranking change rate sequences to the MM paths.
c. Predictions with racer
Assume m+2 temporally successive crawls with respective snapshots. For each Web page, assuming it survives in all graph snapshots, a sequence of m+1 racer values can be constructed. These sequences are used to construct an m-order Markov Model (MM) for some fixed m. After computing transition probabilities for every path, using the generated racer sequences, the future racer values can be predicted using the chain rule: we predict the most probable value X based on the equation X = argmaxX P(a1 → … → am → X) where ai = racer(pj, ti), i.e., the racer value derived from snapshots ti and ti+1 for a page pj. Thus, we are able to predict future racer values for each Web page pj and therefore the future ranking position of pj.
3. EXPERIMENTAL EVALUATION
We performed experiments on two real-world datasets: a bibliometric citation graph derived from DBLP and a subset of the European Internet Archive. In our experiments, we evaluate the prediction quality in terms of similarities between the predicted top-k ranked lists and the actual ones, with two classical similarity measures for comparing top-k lists [3]: OSim (that captures the degree of overlap between the lists) and KSim (that captures the degree of agreement between the lists).
We built a graph structure from the DBLP dataset as follows: Nodes of the graph represent a publication and Edges represent the citations between papers, creating thus twelve snapshots of the graph corresponding to different time periods. Note that the structure of the DBLP graph is highly similar to the Web graph, while having the specificity that no links can appear for old papers to new papers. The Internet Archive dataset comprises of approximately 500,000 pages and refers to weekly collections of eleven UK government websites. We obtained 24 graph snapshots evenly distributed in time between Mar. 2004 and Jan. 2006.
We evaluate the prediction performance of the prediction framework involving both datasets. We also consider a baseline prediction schemes, static, that just returns the top-k list of the previous snapshot (i.e., we consider that all pages remained at the same rank). We computed PageRank scores for each snapshot of the DBLP and Internet Archive datasets, ordered the pages and calculated the racer values for each pair of consecutive graph snapshots. Based on these partitions, we constructed m-order MMs for m ∈ {1,2}. Then for each page p we predict a ranking which is compared to its actual ranking after using 10-fold cross validation.
In Figure 1, we present the prediction accuracy of the framework for 1st- and 2nd-order MMs, compared to the static baseline scheme. The prediction quality is depicted by the respective OSim and KSim values. For each experiment we calculate the similarity between the predicted and the actual ranking and measure the prediction quality for various top-k lists, 10 ≤ k ≤ 300. The first two graphs of Figure 1 illustrate the predictive quality of the framework for the DBLP dataset, the first one with OSim and the second one with KSim. In both cases, our predictions outperform the baseline. Our predictions for the Internet Archive dataset can be seen in the last two graphs of Figure 1. Again the proposed framework outperforms the static baseline for both similarity measures. The 2nd-order MM performs systematically better than the 1st-order MM.
4. CONCLUSION
In this paper, we propose a method for predicting the future rank of a Web page. We conducted experiments on real-world datasets that yield very encouraging results, achieving high prediction accuracy. Our predictions outperform the various baseline approaches we have adopted for all similarity measures and MM orders, across all datasets used. This framework is thus a meaningful tool for rank predictions in the Web graph. Further work will focus on the following issues: i. Conduct experiments for query-based ranked lists, ii. Elaborate on statistical learning methods for a priori selection of the optimal MM parameters.